Swiveling Heads

Swiveling Heads

From: dbhguru@comcast.netTo: entstrees@googlegroups.comSubject: [ENTS] Equipment comparisonsDate: Sat, 3 May 2008 01:01:41 +0000

ENTS,

One of the projects on the ENTS drawing board is an in-depth evaluation of the laser equipment we use in measuring trees. In the past, many e-mails have been passed through the ENTS list on the subject of laser accuracy, but at least in my case, experimental controls have seldom been up to research standards. It is time that I remedied that situation. So, in the coming weeks and months, expect a lot of information and requests for suggestions on how to proceed with testing.

I plan to get another Nikon Prostaff 440. One can't have too many. Now that the canopy is starting to fill out, the value of my TruPulse 200 and TruPulse 360 is limited. Those two expensive lasers just won't thread the needle and shoot through small openings. It is frustrating. I'm going to try both with a tripod to see if I can zero in on a spot, but I'm not expecting a change of penetration capability. In my view, the lack of penetration capability is the chief weakness of the TruPulse line.

Bob

==============================================================================
TOPIC: Equipment comparisons
http://groups.google.com/group/entstrees/browse_thread/thread/9dd49f98649a8c8a?hl=en
==============================================================================

== 1 of 1 ==
Date: Fri, May 2 2008 7:36 pm
From: DON BERTOLETTE

Bob-
Some years back, in looking for solutions to problems I anticipated but never had to rectify, I looked into a monopod/tripod-based system. I was looking for an all-in-one digital solution that though costly, would gather and record digital data in the field, such that in returning to camp, one just downloaded data into a laptop (a 'mother tanker', if you will). Each day was recorded, and at the end of the week, data was downloaded to an office desktop for inclusion into a GIS. That way, data was backed up daily, and there was always more than one copy.

Your elevation of field data collection to a research standard is laudable. IMHO, one of the few chinks in the ENTS Dendromorphometry armor is the pivoting of the handheld vertical angle measuring device (clinometer, whatever). Using a monopod/tripod based system will go a long ways towards tightening that slack.

Another advantage is use of one of Laser Tech's or other's fluxgate compasses, which enable digital recording of horizontal angles. This would help nail down locations that GPS's don't function well in due to large tree crown cover. Finding a GPS-ed location within sight of the candidate/OG tree would nail down locations that would most likely meet Gary's GIS standards. Establish three points on line, occupy middle point, take fluxgate compass readings on all three, you've an angle, shoot a laser distance, and you've a vector.

I would think that if you want to challenge acamedicians on replicable data, the cost of these devices would be justified.

I bet there are even grants available to support the mission!
-Don

==============================================================================
TOPIC: Equipment comparisons
http://groups.google.com/group/entstrees/browse_thread/thread/9dd49f98649a8c8a?hl=en
==============================================================================

== 1 of 1 ==
Date: Sat, May 3 2008 9:36 am
From: dbhguru@comcast.net

Don,

The swiveling head problem is duly noted, but I presently don't believe it is a source of major measurement error. I'll present a mathematical argument to that effect in a coming e-mail. If the argument turns out to support your contention, I'll make special note of that. This said, if the swiveled head source of error can be controlled, I would certainly not argue against doing so. At present, equipment cost is the biggest consideration, and I don't know how, for the membership at large, to get around the financial challenge. I have plenty of sophisticated gizmos and plan to add more, but I'm fortunate in that respect. Ents on slimmer budgets who nonetheless have major contributions to make to the ENTS database will have to have a low cost solution.

In terms of the scientific value of our data, as it stands now, we can build a strong case to be within +/- 1.0 feet of tape drop height with about a 90% probability (not based on a single measurement). That accuracy is across the board - not just for compliant trees such as straight-boled conifers. However, a more complete investigation of the sources of measurement error and their quantification via probability theory will be part of the dendromorphometry book. It is not going to be an insignificant work - nor an easy one, but all the coauthors expect it to be the seminal publication on the subject both at practical and theoretical levels.

The replicable data argument you make is a good point. For one thing, fine tuning our controls is necessary to gain accurate baseline measurements that don't necessitate tape drops. BVP talks about measurements that Chris Anderson (hope I have the right person) has done on Redwoods that are accurate to +/- 1.0 centimeters. Talk about accuracy! Bob says that Chris won't even think of measuring if there is the slightest stirring of a breeze.

Bob

== 2 of 5 ==
Date: Sat, May 3 2008 2:06 pm
From: DON BERTOLETTE

Bob-
I realize we're talking small potatoes here...but the same doggedness that has you backing up to the 'clickover' would seem appropriate in getting as accurate AND precise a measure of the champion tree as is possible with the equipment employed.
As I reviewed your description below, I almost came to the conclusion that the same angle was being measured, just 3-5 inches ahead (similar triangles). Without a "CSI" mannekin with laser pointer modelling this, I want to say that the angles of incidence cross in the 1-3 inch portion.
Cost an issue? Absolutely. Not available to the average guy, not even the average legendary ENTS-person. As a government employee considering at the time a similar number of trees to be measured (thousands), it made sense to purchase one or two such devices. But with ENTS satellites such as you've arrayed, it would clearly be cost-prohibitive for any more than that, UNLESS YOU WERE ABLE TO LINE UP FEDERAL/NGO grants....:>}
-Don

== 3 of 5 ==
Date: Sat, May 3 2008 2:20 pm
From: dbhguru@comcast.net

Don,

Understood. Any ideas on how to go for such a grant? I'm a neophyte in that area.

Bob

== 4 of 5 ==
Date: Sat, May 3 2008 4:05 pm
From: DON BERTOLETTE

Bob-
Causes...the better the cause, the better the chance of getting support financially.
While ENTS objective may be to obtain sufficient funding to purchase the "dream team of lightweight, easy to carry, accurate-as-can-be devices to measure champion trees, if ENTS couches such an enterprise in objectives such as research to explore the relationship of old-growth trees to watershed quality, and requires accurate equipment to assess the structural quality of old-growth in watersheds, there may be a bunch of entities, agencies, organizations that would like to underwrite that. Of course, you'd have to provide the granting agency with 'deliverables', such as GIS mapping of spatial relationships of OG (by whatever definition that works for the agency, per Lee's definition...;>).

I've created a quick scenario that would be favorable from ENTS perspective. But that's backwards.

The more productive technique is to go to a list of granting agencies, find a group of scenarios that best fits ENTS needs, then start filling in the blanks...it's not quite that easy, but I thought it might be good to getting things started...a number of your academicians are likely soft-funded, and rely on grants for research...guys like Frelich, Leopold, Dunwiddie, Cogbill, etc. likely have such a list of granting agencies, etc. Competition can be fierce, and wordsmiths win.-Don

== 5 of 5 ==
Date: Sat, May 3 2008 6:15 pm
From: "Edward Frank"

Bob and Don,

If I may ask at what point in the rangefinder or in your head is the base point from which the actual distance to the object being measured. It would seem to me that whatever that point is, that should be the point at which the effects of swivel should be calculated.

Ed

== 4 of 15 ==
Date: Sun, May 4 2008 7:14 am
From: "Edward Frank"

Don and Bob,

I don't think either of you are visualizing the mechanics properly. Consider a measurement consists of two values 1) distance, and 2) angle. These are broken down into a top measurement and a bottom measurement. ANGLE: when you measure an angle you are looking through the clinometer. You tilt your he and up and down when you make these measurements. The actual vertex of this triangle, is not you eyeball, but the point where your head pivots. This is somewhere around just back of your ear. The angles are correct with respect to this pivot point as they are simply points along the arms of the triangle whether at the actual base or along the arms. It makes no difference. DISTANCE: The measurement is distance to the top or base of the tree. Say this is measured at the front of the rangefinder where the sensor is located. This point moves up and down as you tilt your head. The math assume that the angles you are using to calculate the vertical offset is taken at the same point as the distance, and that distance is taken from a fixed point also. Since the measurement point in the rangefinder is being moved up and down as you tilt your head these parameters are not being met. A simple diagram shows that the actual height will be offset (shorted) by the amount of the vertical movement. You would get parallel lines with the base angle and that same base angle offset upward by the amount of vertical movement of the rangefinder sensor between the upper and lower readings. In addition this amount of movement would be variable dependent on how much you have tilted your head. This is what you have figured out so far right?

This is where the visualization problem has occurred. The problem is not that you have moved the instrument's measuring point up and down. It is that you are using the the wrong distance value. The distance to the object is the distance from the measuring point on the instrument PLUS the distance between the measuring point and the pivot point in your head. The latter is a constant. By correcting this distance, it doesn't matter that the instrument moves up ad down, because then the angles measured and the distances measured both are referenced to the same constant vertex point. You simply need to correct the distance being measured by this constant and all the other variable go away. (hint -calibration table)

Using the instrument on a tripod is much ore complicated mathematically as everything is so much simpler with the pivot point being behind both instruments.

Ed

== 5 of 15 ==
Date: Sun, May 4 2008 7:43 am
From: "Will Blozan"

Ed, Bob,

I suppose you would need to find click-over on the laser as it sits
stationary (like on a table shooting horizontally) and then measure back
towards the laser with a tape the same distance from the target. Ideally
this point would be at the eyepiece of the device. If it was in front or in
back of the laser you would have some significant errors to contend with.
But on the bright side, this may be the most accurate way to calibrate and
compensate for head tilt and "laser origin offset" for lack of a better
term. However, clinometer error, hand shake etc. would likely negate all the
fine details at the "head".

Will

== 6 of 15 ==
Date: Sun, May 4 2008 8:01 am
From: "Will Blozan"

ED,

I disagree. If you were measuring a tree in which you were dead-level with
the base why would you need to "add" the distance "below" the laser to the
point of the vertex of the triangle behind you? Clearly you are not below
the tree, so adding any distance (height) does not make sense. Maybe I
missed something?

Will

== 7 of 15 ==
Date: Sun, May 4 2008 8:38 am
From: "Will Blozan"

Hey all,

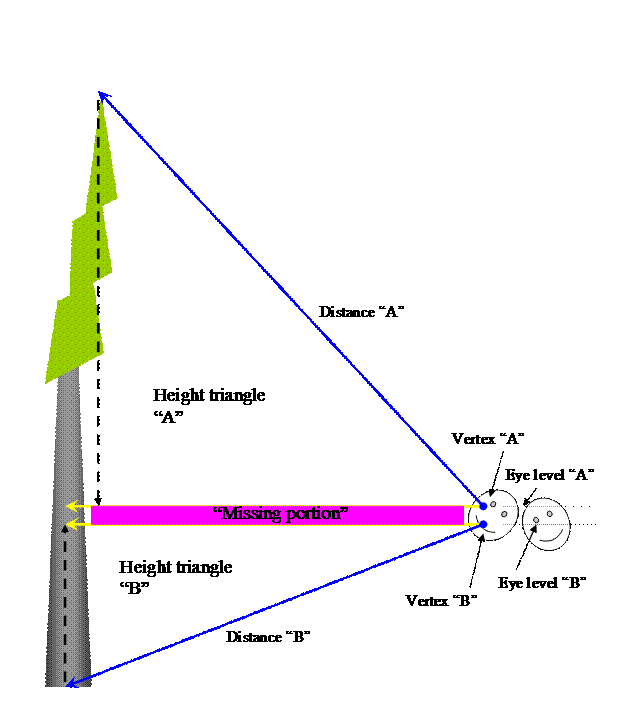
The PINK region in the diagram above represents the "missing" portion not
measured in the height triangles originating at the vertex of "A" for the
top shot and "B" for the base shot. Distances "A" and "B" are from tree TO
eye (laser) and angle is FROM eye, not anywhere behind the vertices. Does
this make sense? The combination of the two angles is artificial; they are
independent calculations and as such stand alone. If we were using the
TANGENT (%) method then we may want to combine the angles and correct for
tilt and a "phantom vertex". But we don't want to go there now do we?

Will

== 8 of 15 ==
Date: Sun, May 4 2008 9:32 am
From: dbhguru@comcast.net

Will,

You beat me to the punch. Your diagram is the one I intended to draw and it is the correct one needed, conceptually, to isolate the missing vertical distance that I was originally talking about. It is true that we can attempt to calculate this vertical missing distance by appealing to the extra distance to the vertex of the projected triangles in accordance with what Ed is visualizing, but it is easier to measure the vertical offset directly. Either way, in the end, we can reduce the unknown to about a inch or two at the most. Given the magnitude of the other sources of error clinometer and laser accuracy, conceptual mathematical model used, I'm content to quickly make a rough calculation of the offset and move on.

Another point to consider about the triangles is that the real ones we have to construct in the fiekd to measure the above and below eye-level components do not necessarily lie in the same vertical plane. From standing in the same spot, when one starts to measure the above and below eye-level components of height, one often must swivel the head laterally when going from the high point to the low point because those points are seldom in perfect vertical alignment with one another. If they were, the tree would be like the proverbial vertical telephone pole in a level parking lot. But trying to align them all so that the base, the trunk, and the high twig all lie in the same vertical plane is a waste of time and unneeded to be able to compute the two components of height.

These subtle points are very much worth us debating, but we need not to ever lose perspective on their contribution to overall error - a subject that I expect we'll spend a lot of time on in the dendromorphometry book.

Bob

== 9 of 15 ==
Date: Sun, May 4 2008 11:38 am
From: Andrew Joslin

I've been thinking of the same problem. To solve that and other "body
mechanics" related errors I'm considering taping my clinometer to the
right side of the rangefinder and then mount the rangefinder on a
light tripod with a fluid head mount. Tripod mount should improve the
precision of clinometer readings as well.

Andrew Joslin
Jamaica Plain, MA

== 10 of 15 ==
Date: Sun, May 4 2008 12:39 pm
From: dbhguru@comcast.net

Andrew,

We're talking about a couple or three inches of possible error, which can mostly be compensated for it simple mesurement of eye drop. By contrast, the traditional clinometer-baseline method often introduces errors in the tens of feet. We certainly want to keep all sources of error in mind, but we also want to keep them prioritized, so we don't over-emphasize a source of error that is pretty well boxed in at a couple or three inches. This said, I would encourage you to follow through with the experiment and report on it to us.

Bob

== 11 of 15 ==
Date: Sun, May 4 2008 12:51 pm
From: "Will Blozan"

Andrew,

I'm sure you are aware of this but the equipment you have does not have the
resolution to justify the miniscule gain in precision all that effort would
require. If you had an Impulse laser or one that has a resolution in the
centimeter range it could be justified. But then you would need to wait for
an absolutely calm day with no sway in the tree.

Will

== 12 of 15 ==
Date: Sun, May 4 2008 3:13 pm
From: Andrew Joslin

That makes sense. I guess the 1/2 yard error in the rangefinder makes
tripod mounting nearly irrelevant.

There are times though when it seems like steadying the clinometer on
a tripod would be helpful for the angle measurement side of things.

Andrew Joslin
Jamaica Plain, MA

== 13 of 15 ==
Date: Sun, May 4 2008 3:22 pm
From: dbhguru@comcast.net

Andrew,

I don't think Will is suggesting that steading the clinometer isn't a good idea, just that elaborate measures taken specifically to reduce the head swivel-associated source of error is probably not a productive use of time. I agree completely with Will on the point.

Bob

== 14 of 15 ==
Date: Sun, May 4 2008 5:43 pm
From: "Edward Frank"

Bob,

Please do the diagram like I suggested. There isn't ANY vertical error involved in the calculation due to the movement up and down of the rangefinder. You do not need to attempt to calculate anything. The entire system of sighting the laser and measuring the distance is based upon that single pivot point of the tilt of your head. The rest of this discussion is therefore meaningless... There isn 't missing vertical distance as shown in Will's diagram. The entire idea is based upon the false assumption that the measuring point is the eye instead of the pivot point of your head.

Ed

== 15 of 15 ==
Date: Sun, May 4 2008 7:15 pm
From: dbhguru@comcast.net

Ed,

I'm starting to work on a simple diagram that should illuminate the variables relevant to our discussion. Hopefully all of us can address the variables by referring to the features of the diagram . I'll send the diagram sometime tomorrow along with a few measurements that I've taken, which the rest of you can then analyze/criticize. In the interim, some key points to be thinking about follow.

1. The position of our instrument(s) in space relative to the target being measured is what determines the values returned by those instruments as read by us peering into an eyepiece. In the case of my Trupulse, the mechanisms for measuring distance and angle are in the same instrument. So, with the Trupulse, I don't have to deal with instruments of different sizes/lengths for measuring distance and angle in considering the impact of head swivel. However, if I use my Suunto clinometer and Nikon, not much changes. The difference in the lengths of the mechnical Suunto clinometer and the Nikon laser rangefinder are almost the same. So, for the purposes of these discussions, I can effectively eliminate instrument length as a variable in the points I will be making.

2. We should think a little more about head swivel as a variable. Swivel occurs from our neck movement. If we swivel our head far enough, we definitely change the horizontal plane of our eyes between higher and lower positions. Of course, in using our instruments, we also rotate our eyes in their sockets to minimize head swivel, but some swivel usually occurs - which is the focus of our discussion.

3. When we look up, if we tilt our head back, the position of our eye and instrument held against it moves back slightly. Conversely, if we look downward, we swivel our head forward and the position of our eye and instrument held against it moves forward slightly. The vertical placement of the instrument also changes as our head swivels. As an extreme example, think of tilting the head backward to look straight up. Then tilt the head forward to look straight down and consider the changes of position of an instrument being held against the eye. There is a small amout of horizontal displacement and a slightly larger amount of vertical displacement in these extreme movements that change the location of the instruments that are doing the measuring.

There may be other considerations, but these are the ones that come immediately to mind.

Bob

==============================================================================
TOPIC: Swiveling heads
http://groups.google.com/group/entstrees/browse_thread/thread/0edddc198240241e?hl=en
==============================================================================

== 1 of 4 ==
Date: Sun, May 4 2008 9:17 pm
From: "Edward Frank"

Bob, Will, ENTS,

I apologize for my hand drawn illustration. ( I overwrote the hand letters with a editing program) I know it is not up to the par of the ones by Will, Bob, and others.

Here is a diagram of two heads - the orange one looking at he base of the tree and the blue one looking at the top of the tree.

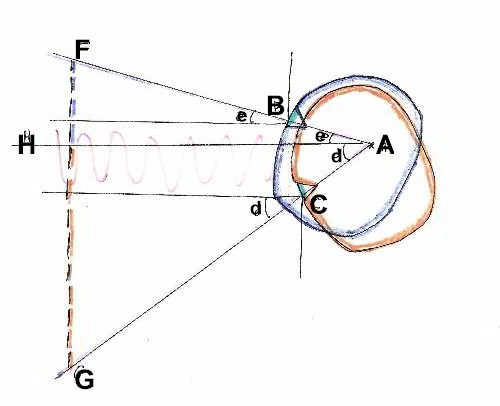
There is a point in the central portion of your head where the head pivots. This is where it is attached to the spine. As you tilt your head up and down this point stays in the same position. This point is marked as A in the diagram.

When you sight through the clinometer or rangefinder you are essentially sighting along a line that runs from this pivot point A through the eye B or C to the target F and G respectively.

Bob and Will have suggested that when you measure a tree there is the distance represented by difference in height of your eye when looking up B and when looking down C. This is marked by the squiggle through the center of the diagram between the two horizontal parallel lines leading outward from points B and C. This is not exactly the case. The angle you measure when looking upward toward the top of the tree F from your upward raised eye B is represented by the angle e. This angle is the same whether you measure it from the surface of the eye B or project it backward to the pivot point in your head. Both triangles formed are similar and therefore the angle e is the same in both instances. A similar argument can be made for the lower half of the measurement to the base of the tree G with the angle both from the eye C and projected back to the pivot point A forming the angle d.

What about the missing height? That is related to the point from which you measure the distance. If you were measuring the distance from the surface of the eyeball, as is assumed by the diagram Will presents, then there is this missing distance, but...

Remember the size of your head does not change as you tilt it, so the distance AB is equal to the distance AC - it is in fact a constant. The apparent difference in height is equal to sin e x distance AB + sin d x distance AC In other words all of the missing height is literally inside your head.

If you look at the mechanics the distance between the position of your upraised eye and down tilted eye changes dependant on the difference between the angles you are using to measure the tree. It can amount to very little to up to 3or 4 inches or so. It will change with every measurement.

However the distance between the front of the eyeball and the pivot point will remain constant. If you project the angles back to this point the lines all converge and there is no vertical offset between looking up and looking down.

This comes down to what point you are measuring your distance from. If the measurement distance to the top or base of the tree is measured from the eyeball, then there will be this vertical offset. If the distance is actually being measured from the sensor on the front of the rangefinder, and you are measuring this exactly, then since it sticks out farther then the vertical offset will be even greater. If the distance is measured relative to the pivot point in the middle of your head, there will be no vertical offset, and no vertical error in the measurement from tilting your head back and forth.

So how do you measure to the point in the center of your head? Easy, when you calibrate your rangefinder - when the rangefinderr hits a click over point measure the actual distance from the target to a point approximately at your ear. Since this is a constant it will not affect the accuracy of your rangefinder readings - it is simply using a different reference point to begin your measurement - not your eyeball but your ear. You will not need to correct for the apparent vertical offset from tilting your head, because there is none at the pivot point. Because the pivot point is behind, but along the same line as you are sighting, the size of your instrument does not make any difference either.

I can try to explain it differently if I am not making myself clear.

Ed Frank

== 2 of 4 ==
Date: Sun, May 4 2008 9:57 pm
From: "Edward Frank"

I guess to summarize: If you choose to measure the distance to the target as AF or AG rather than BF or CG, then you do not need to correct for the vertical offset from moving your head. All of the variables are eliminated because the lines converge at point A.

== 3 of 4 ==
Date: Sun, May 4 2008 10:05 pm
From: "Edward Frank"

There is not a need to correct or consider the apparent vertical offset because by adjusting the distance to the correct point - the pivot point inside your head -the "offset" is already included in the basic calculation. Sorry for dribbling these things out - it is 1 in the morning and I am sick and I am leaving out these obvious comments....

== 4 of 4 ==
Date: Mon, May 5 2008 12:17 am
From: dbhguru@comcast.net

Ed,

Your diagram is clear and the explanation you give is equally clear. I've basically understood the argument you've been making from the beginning and your drawing and latest explanation confirm it for me. The area where we differ is explained as best as I can at 3:00AM as follows.

I'm unsure if point A in the diagram stays fixed in location. Stated another way, I'm unsure if the action of the head is as mechanical as depicted, at least for some of us. I have a tendency to lean forward or backward when looking down or up (swaying) and I think I flex more of the spine than is depicted by pivoting in the drawing from a single point at the top of the spinal column. I guess I make a lousy human tripod. I've stood with my back to a wall with my head touching the wall so that I am standing perfectly vertical and all points are in vertical alignment. When I look down, using a head swivel action, my head comes out of contact with the wall, moving forward and down. I'm not just pivoting from point A as located at the base of my skull. Point A moves a bit. Tilting my head backward is less of a problem. I can do more of the pivot that is depicted in the diagram, i.e. swiveling around point A. I've understood this about my posture all along. That is why I try to be
very conscious of the position of my instruments.

The issue comes down to the position of point A in the head when the head is tilted forward or backward. Imagine someone with a stiff neck. How effectively do they pivot from a fixed point? I'm unsure if my stance is atypical or not. Maybe I'm too inflexible, but the point A that is supposed to stay fixed does so - not absolutely. Other than that, I agree that the extended distance to a common vertex at point A works to eliminate the need to compensate for the change of location of one's instrument if otherwise standing in a fixed location and swiveling the head around point A as shown.

There is another point to be made here - a very practical one. In actual tree measuring situations encountered in a closed canopy forest, you not infrequently find yourself in a situation where positioning yourself to see the crown point sufficiently clearly doesn't allow you to view the base or vice versa. Shifting laterally becomes necessary, often by more than just a couple of feet, so that shooting from different positions on the same or parallel horizontal planes becomes more than an abstract concept. I've had to set up a pole to mark the eye level spot where I shot the crown or base and then shifted to a new location where I could see the other extremity of the tree. Finding and measuring the absolute top and base of a tree in a closed canopy forest is often more labor intensive than casual measurers will tolerate. One becomes adept at putting into practice measuring the vertical distances between three or even four (though rarely) parallel planes.

I'm anxious to hear what Will and others have to say on the inflexible spine problem. I'm off to bed.

Bob

== 3 of 14 ==
Date: Mon, May 5 2008 6:04 am
From: Beth Koebel

Bob,

I understand the point that you trying to state.
There are times when I look up and I have to place a
foot backwards to steady myself. I of course then
start all over.

Beth

== 4 of 14 ==
Date: Mon, May 5 2008 6:17 am
From: "Edward Frank"

Bob,

You wrote: "There is another point to be made here - a very practical one. In actual tree measuring situations encountered in a closed canopy forest, you not infrequently find yourself in a situation where positioning yourself to see the crown point sufficiently clearly doesn't allow you to view the base or vice versa. Shifting laterally becomes necessary, often by more than just a couple of feet, so that shooting from different positions on the same or parallel horizontal planes becomes more than an abstract concept."

Yes these are other potential types of error and not related to head tilt error.

Ed

== 5 of 14 ==
Date: Mon, May 5 2008 7:56 am
From: dbhguru@comcast.net

Ed, Beth, Will, Don, et al.,

As best as I can determine from experiments on myself, the swivel point of my head at the top of my spine doesn't stay absolutely fixed in location, although, I concede to you, Ed, that the movement is small enough that it can probably be ignored in most cases. In those situations, Ed, your model is correct and your point is duly acknowledged. In a large number of in-forest measuring situations, it is more of a dice roll, though. Standing on a rock, log, or unlevel ground causes me to sway a little, changing the location in space of point A, but as you correctly say, Ed, the key is the amount of vertical movement as opposed to horizontal movement of point A.

Another consideration is the parts of the body that are involved when we move our head forward or backward. I don't think that the movement is just from the head swivel portion alone - at least not in my case. I can't speak for others. The neck vertebra seem to come into play, albeit by a small amount - but if were going to thread needles, let's thread them all.

Of far more practical concern to me is the wide variety of in-forest situations that I encounter where some body movement other than head swivel becomes necessary. When going from measuring the crown to measuring the base, the visibility of both from the exact same stance may not be sufficient to get laser returns. For me, this has proven especially true for the TruPulse, not so much for the Nikon, somewhere in between for the Bushnell lies, and forget the Optilogic. Long ago the visibility challenge of in-forest measuring in highly cluttered environments pushed me into adopting the concept of vertical distance between the horizontal planes model that I speak to frequently. A very narrow opening to either the base or crown with concurrent lack of visibility to the other spot from a fixed head position is what I'm speaking about. Loss of visibility at one end of the tree or the other can lead to the necessity of constructing the height of the tree in three or possibly more piec
es. Poles and reflectors can reduce the frequency of occurrence of this type problem, but not invariably. I have been forced to resort to piecing together a height of a tree where forest clutter is an intractible problem.

There is still another consideration, though one that does not necessarily negate your diagram, Ed. It is seldom that we line up the highest crown position, the base position, and the eye in the same vertical plane, since there is no necessity to do that in sine-based math. The head often swivels to the side to pick up the crown or base point relative to the other. I acknowledge that this doesn't necessarily cause point A to move, but some largely unconscious change of body position that effects the location of point A can occur. This argument may sound unnecessarily picky, but as I said previously, if we're going to thread needles, we should thread them all.

While on the subject, another source of a shifting location for point A comes from trying to measure top and bottom of a tree from laser clickover points. The ground location of the clickover for the crown does not always match that for the base. In fact it often won't. Long ago, we had many ENTS e-mail communications on this subject. From the first clickover point, one may have to move forward or backward to find the alternate clickover spot, which obviously shifts the location of point A. When not on level ground, there is a vertical component of the shift as well as the horizontal one and getting the clickover spot right is pretty important to minimizing laser distance error.

Given all the variables, I've often thought that we should give a +/- value to accompany each height measurement. This would generally be anywhere from 0.5 to 3.00 feet depending on how many precautions we took and how much statistics we brought to bear.

Well, I'll let it go for now. I imagine Don Bertolette wishes he'd never broached the subject.

Bob

== 6 of 14 ==
Date: Mon, May 5 2008 8:21 am
From: "Edward Frank"

Bob,

There still seems to be some disconnect here. Without regard to any other movement of the head, the amount of vertical "apparent offset" introduced by tilting you head is = sin angle x the distance from your eye to the pivot point, both up and down. That distance is always the same because they are fixed points in your skull. The amount of apparent offset is dependant on the distance from the pivot point. The farther away from the point the greater the apparent offset. This offset goes to zero at the pivot point. By using this fixed constant distance as part of your distance calculation, there is no vertical offset from tilting your head. Other movements may add errors, but there is none from tilting your head.

I am sorry to keep repeating this, but I am just trying to keep you and your covey of colorful characters from crazily careening off course and crashing as you craftily conceptualize dendromorphometry calculations.

Ed

== 7 of 14 ==
Date: Mon, May 5 2008 9:37 am
From: "Edward Frank"

Bob,

I agree that there should be error bars in our measurements. The question is how to determine how much they should be. I don't think it should be the sum of the maximum possible theoretical error in each stage of the process. Some of the errors are likely of the kind that are either/or but not both. Not all of the errors would be maximized at the same time. Not all of the errors would have been in the same direction. Figuring out what they all might be is a step in the right direction.

Might I suggest a pragmatic approach to the error question? We have a number of trees that Will has climbed and measured by tape drop and which he has also measured the height via laser/clinometer. Will is meticulous as you are yourself. Therefore a good range of error bars might be based upon the real world examples of the difference in Wills' laser measurements and his tape drop measurements. You would only need to eliminate those cases where the tape drop was from a different top than the one lasered. This was the basis of compiling the measurement error tables on the website initially. He should have more data from the recent hemlock studies that could form the core of the data set?

Ed

== 9 of 14 ==
Date: Mon, May 5 2008 1:00 pm
From: DON BERTOLETTE

Bob-
Actually, I've appreciated the thought provoking responses from folks. I like your comment about range of errors (confidence level) being attached to the reading, to more comprehensively address accuracy and precision issues.
It allows a little wiggle room for another 'niggling' source of error...the diurnal/seasonal expansion and contraction of a large tree as it varies between turgid and flaccid states, reflecting different atmospheric moisture relations/soil moisture content...:>}
-Don

== 10 of 14 ==
Date: Mon, May 5 2008 1:13 pm
From: dbhguru@comcast.net

Don,

Good points also. For some time I've been uncomfortable with a stated measurement carried out to a tenth of a foot without some qualification as to accuracy range tied to a probability. I know that I range from +/- 0.25 to 2.0 feet depending on how much time I take and whether or not my equipment is calibrated. On occasion, everything goes south with a measurmeent and I'm off by close to 3.0 feet, usually when my laser is having difficulty with clutter. As the leaves start to develop on trees, I'm seeing the tradeoff against a larger brighter target and clutter. I also have confirmed that the TruPulse has much greater accuracy problems if the sky beyond the target is bright blue. If it is cloudy, I get the best laser responses.

There is also the experience factor. In North Carolina, I shot a tree in front of the lodge in which we were staying. Will walked over and I said: "Take a guess on the height of the tree I just measured." He did and was off by only 0.2 feet! I've seen him do that more than once.

Bob

== 11 of 14 ==
Date: Mon, May 5 2008 1:21 pm
From: DON BERTOLETTE

Bob, Ed, Beth, Will-

I have no intention of preaching to the accuracy choir here, just applying my surveying background. Like Jack (!) Sobon, when I think of angular accuracy, vertical and horizontal, I'm thinking transits and theodolites. For me, the clinometer is a forester's field tool, designed to get reasonably accurate estimates of vertical angles quickly.

And the clinometer has served that role well, and with a cost-effectiveness that has allowed many fieldbound folks to get in on the fun. Countless millions of vertical angles have been taken over the years~

I don't have a really good sense of the number of tree heights that the ENTS database has, and what percentage of them need the centimeter accuracy. If it were a relatively small number, say the trees that are likely candidates for champion tree status, I'd suggest that it might be worth the trouble to use survey grade equipment such as a Total Station which measures distance with laser, and angles vertical and horizontal to a high degree of accuracy. I recognize that there are issues of underbrush to overcome.

As a surveyor having gone through manzanita and mountain mahogany before the era of electronic distance meters, it only takes a fist size hole through the brush to get a good reading. Of course this would be worth the trouble, only for a relatively small number of candidates, and most likely on a rental basis (a Total Station can be rented in most any reasonable sized city).
-Don

== 12 of 14 ==
Date: Mon, May 5 2008 1:26 pm
From: DON BERTOLETTE

Bob-
While I don't know that I could have matched Will on my best day, but one does ''develop and eye'' for heights and breadths, when measuring many of them.
Re blue sky versus overcast sky, I was surprised with your comment, I would have thought the opposite. Do you suppose it's an issue related to the electromagnetic spectrum (what the human eye can see, versus what wavelengths the laser is encountering)?
-Don

== 13 of 14 ==
Date: Mon, May 5 2008 1:29 pm
From: dbhguru@comcast.net

Don,

You make a good suggestion. Yes, it was Jack Sobon and his transit that made me see the light. Transits are way cool.

Bob

== 14 of 14 ==
Date: Mon, May 5 2008 1:31 pm
From: dbhguru@comcast.net

Don,

I don't know what it is. However, Laser Tech did tell me that shooting against a bright blue sky was the toughest - the opposite to my Bushnell. Like you, I thought it would be the reverse.

Bob

== 2 of 2 ==
Date: Mon, May 5 2008 1:27 pm
From: DON BERTOLETTE

Bob-
Done!
-Don

== 4 of 8 ==
Date: Tues, May 6 2008 11:20 am
From: doncbragg@netscape.net

ENTS--

Keep in mind that when trying to determine errors, tapes can have problems as well--cloth tapes can be stretched by years of use, abrasion of the materials, etc., and metal tapes are potentially sensitive to changes in their temperature.? These influences may not be major, but they are not necessarily trivial, either.? A difference (between a laser measure and a tape drop) of a few inches on a 150+ ft tall tree could arise from errors in tape length...

Don

~~~~~~~~~~~~~~~~~~~~~~~~~~~
Don C. Bragg, Ph.D.
Research Forester
USDA Forest Service
Southern Research Station
~~~~~~~~~~~~~~~~~~~~~~~~~~~

The opinions expressed in this message are my own, and not necessarily those of the Southern Research Station, the Forest Service, or the USDA.

== 5 of 8 ==
Date: Tues, May 6 2008 1:27 pm
From: "Will Blozan"

Don,

True, but I challenge anyone to stretch a 150' fiberglass tape a few inches!
It will snap first. The weight of the tape (~.5 lbs maybe) during a tape
drop would result in infinitesimal stretch. All tape drops I do are recorded
to the nearest 0.1 feet (1.2 inches) so resolution is not even close enough
to consider any minor stretch. Far more important but not super-significant
is the tape not being vertical.

Will

== 6 of 8 ==
Date: Tues, May 6 2008 4:34 pm
From: DON BERTOLETTE

Will-
I know that you were referring to Don C. Bragg. For those of us who have surveying backgrounds where distances are measured and recorded and become the law, there are ways to measure under controlled conditions...a surveyor often measures distances with a steel tape, that can be corrected for temperature, distance, slope...to hundredths of a foot (in most cases, within less than an inch).
Extreme? You don't know until it's been assessed then either adopted or tossed. If ENTS is to be the premier tree measuring entity, it should consider some of the traditional superlative measuring technologies.
Laser distance metering? In the 1980's I was using Hewlett Packard Electronic distance meters (survey grade) to measure distances up to three miles, accurate to within hundredths of a foot, albeit with parabolic reflectors (back then it took a triangular array of three "triples", each lens 2 1/2" diameter). For the level of distance measuring accuracy that ENTS folks should be considering, a 2 1/2" single parabolic lens, or even a 1" parabolic lens (very light, easy to carry) should be tested (they're always the same, as opposed to different readings from different surfaces). If difference between existing ENTS methods are neglible, then toss the parabolics. But test them first, they really shouldn't be dismissed out-of-hand...
-Don

==============================================================================
TOPIC: Ed wins!
http://groups.google.com/group/entstrees/browse_thread/thread/60f0e18189817884?hl=en
==============================================================================

== 1 of 3 ==
Date: Tues, May 6 2008 2:54 pm
From: "Will Blozan"

Bob, Ed,

I do not concede yet. I doubt anyone's head moves at a pivot point that
coincides with clinometer measurements. Sometimes, perhaps occasionally yes,
but not enough to bank on or maintain as convention. My earlier argument
about using a single triangle to measure a tree at eye level stills hold
some weight, I think. Why would you EVER add on height to a point (vertex)
based on the eye level where the laser AND clinometer measurements are
taken? This is exactly what Ed is suggesting, provided I understand the
premise of his diagram and arguments.

To me, an ENTS sine measured tree is based on TWO triangles totally and
completely independent of each other. The same vertex for both triangles is
neither necessary nor satisfied in my opinion. I see the points made but
realistically don't think they practically apply to what we do. I am not
going to add a few inches to my measurements to compensate for the distance
from eye to "pivot point". Again, the equipment we use is way too coarse for
this exercise. If we were to use to instruments with a much higher
resolution than of course it would need to be mounted on a tripod and
pivoted from the same point. Still, the concept baffles me.

Will

== 2 of 3 ==
Date: Tues, May 6 2008 3:03 pm
From: "Edward Frank"

Will,

This is not what I have suggested at all. Not even close. I don't know what you are talking about, so you must not be understanding the argument and diagrams. I don't know how to explain it any better.

Ed

== 3 of 3 ==
Date: Tues, May 6 2008 4:56 pm
From: dbhguru@comcast.net

Will,

What I conceded to Ed was that if the head swivels flawlessly and mechanically, Ed's correction works to compensate for swivel. Do I believe that the head swivels flawlessly and mechanically? I'm not yet ready to concede that, but am willing to try some experiments to analyze the swivel under a wide variety of head swing situations.

Your emphasis on the two triangle solution we use to measuring tree height is important for everyone in ENTS to understand. We will emphasize this point in the dendromorphometry book.

Bob

==============================================================================
TOPIC: Ed wins!
http://groups.google.com/group/entstrees/browse_thread/thread/60f0e18189817884?hl=en
==============================================================================

== 1 of 2 ==
Date: Tues, May 6 2008 5:28 pm
From: "Edward Frank"

Will,

On this point you are likely right. The pivot point may be some distance say a half inch (just guessing at a number) below the line of sight, and not directly in line with the eyeball, but it is close. The theoretical pivot point will be the same amount off in every reading because it a skull attachment point. It will just form a smaller set of similar triangles and not really affect the measurement as far as I can see. It doesn't really matter very much of the point moves forward or backward or sideways as you take your rangefinder reading, because the distance is measured by the rangefinder in front of you eye and any back forth movement is already incorporated into the physical measurement. The key is in my mind that the pivot point is fixed position with respect to the eye, and doesn't really move up or down as you tilt your head.

I am not determined to be right, I just want this aspect of the measurement mechanics to be understood correctly, whether it makes an actual difference in the readings or not because of the small scale of the errors involved. The mechanics of what is happening is crystal clear to me, I am sorry I can't explain it better so that you can either agree or find where I have made an error in the thinking. I am interested in what you think about the process, I just don't think we are on the same page yet, for better or worse.

Ed Frank

----- Original Message -----
From: Will Blozan
To: entstrees@googlegroups.com
Sent: Tuesday, May 06, 2008 5:54 PM
Subject: [ENTS] Re: Ed wins!

Bob, Ed,

I do not concede yet. I doubt anyone's head moves at a pivot point that coincides with clinometer measurements.

== 2 of 2 ==
Date: Tues, May 6 2008 5:36 pm
From: "Will Blozan"

You are extrapolating a point below the eye. This is what I mean by "adding height".

From: Edward Frank [mailto:edfrank@comcast.net]
Sent: Tuesday, May 06, 2008 6:20 PM
To: Blozan, Will
Cc: Leverett, Robert
Subject: Tilting heads

Will,

I am not trying to add any height anywhere in my arguments or diagrams. In your diagram you show an area marked in pink as "missing height." I am saying that height is not missing at all. I am arguing that the baseline distance for you sighting of the clinometer and the rangefinder isn't the surface of your eye as shown on your diagram, but is really the point at which your head pivots. The argument shows that the vertical component of this portion of the baseline distance is equal to the amount of "missing height" in your diagram, therefore that height is not missing at all. I am not saying anything needs to be added to the height as a correction. The upper and lower triangles are still independent, so I don't see what it is you are saying. I am not determined to be right, I just want this aspect of the measurement mechanics to be understood correctly, whether it makes an actual difference in the readings or not because of the small scale of the errors involved. The mechanics of what is happening is crystal clear to me, I am sorry I can't explain it better so that you can either agree or find where I have made an error in the thinking. I am interested in what you think about the process, I just don't think we are on the same page yet, for better or worse.

Will Blozan writes:

Ed,

I need to know why you think the apex of the triangle is not the eye. The laser is held to the eye as is the clinometer. I can see that if sighting level with the base of a tree your head (and eye level) would shift upwards a bit when you sighted the top. Maybe this is the heart of the issue.

Will

From: "Edward Frank"

Will, Bob,

I am extrapolating a point behind and in line with the eye not below the eye. Look at it this way. When you look up at a tree your head and eyes are tilted upward. When you look horizontally your head and eyes are level. When you look at the base of a tree your head tilts downward and you eyes have moved downward. (in the example I am using for the purposes of illustration, I am saying you are above the base and below the top) The position of the eye has changed as you move your head up and down. OK we both can see this I guess. In your diagram you have labeled this small distance as a missing height in the measurement. OK, you marked this on your diagram so you should see this.

What happens if you continue the line of sight you are using to measure the top angle through your eyeball and out the back of your head. You can do the same for when looking horizontally, or when you are looking down. I am saying that these three lines will all converge at a single point either at which your head pivots. Looking at both the top and bottom triangles together, when you draw them, there is basically a missing top to the triangle formed by the line of sight pointing to the top of the tree and the line of sight pointing at the base of the tree. Your diagram is on the website at: http://www.nativetreesociety.org/measure/swiveling_heads.htm The missing top of the triangle, the portion of these different lines of sight missing from the drawing, is the portion of the baseline that extends into your head. You know these lines will converge beca use the position of the eye in the skull is a fixed point. Any titling action has an axis of rotation, that is the pivot point. The same is true if you use a horizontal plane that can be shared by both the top and bottom triangles. If the projection to this point forms a the tip of this simple triangle, then the distance measured to the target should use the same reference point.

Think of it in a different way. You have formed a right triangle with one arm extending from your eye to the top of the tree when looking upward. The baseline of the triangle is from your eye along a horizontal plane. Your diagram shows a pink space. The base of the true triangle, as calculated using the sin method, for an eye position looking upward would not be at the point the head has turned down to look horizontally, but along a horizontal plane/line at the position of the eye when tilted upward. This would be along the top edge of your pink area, not at the plane of the eye when looking horizontally in the midst of the pink area. This is the upper part of the missing height in your diagram.

This is where the intuitive jump takes place. The triangle formed by the position of the eye as tilted upward for the upper arm, and the horizontal plane at the height of your eye when looking upward forms a nice basic, complete triangle. What happens when you project the line of sight along the upper edge of the triangle, the one pointing to the top of the tree, all the way back until it meets the horizontal plane formed by the eye level position of head when it is looking horizontally? This will form two similar triangle. Both share the upper arm of the triangle, and the base of the upper edge of your pink area (horizontal line at the level of the eye when tilted upward) and the horizontal plane formed when the head is held level, are parallel. Do you see that this forms two similar triangles? Now you can do the same for the lower triangle, where the base of the pink area is a horizontal plane level with the position of the eye when l ooking downward.

When you add the heights of the top triangle and the bottom triangle,you have a height of the tree, except for the small distance between the position of the upward looking eye and the downward looking eye. I think you understand this because that is what you show on your diagram. This distance is variable depending on how much tilting is done between the upper eye position and the lower eye position. Why you have this"missing height" is because the top triangle and the bottom triangle do not share the same horizontal plane when doing the calculations. By projecting the line of sight for both the top triangle to the horizontal plane formed by the level of the eye when looking horizontally, and projecting the line of sight for the lower position to the horizontal plane, you are referencing the measurement triangles to the same horizontal plane. Since they are sharing the same horizontal plane there is not gap or missing height in the calculat ions (between the upper horizontal plane and the lower horizontal plane - the top and bottom of your pink area in your diagram).

The projection of these lines to the now shared horizontal plane formed by the position of your head when looking level, converge at the pivot point inside your head. Since the triangles formed by these projections are similar - the angle for sin top and sin bottom are the same for these similar triangles as they are for the triangles formed at the position of your eye. The only difference is the length of the arms of the triangle along the line of sight to the top and along the line of sight to the base. If you use the length of the lines to this convergence point, the pivot point, instead of the distance to your eye, there is no gap between the upper and lower triangles, there is no missing height. Both of these two new similar triangles encompass the height of the tree in its entirety. This is accomplished by accounting for the distance between your eye and the now shared, common horizontal plane.

This distance is a fixed amount for both the upper angle and the lower angle because you head is rigid. By incorporating this constant into your measurement calculations, or in the calibration of the instrument, the problem of the pink missing height is no longer present. It is better, I think, to add a constant as a correction in your baseline distance measurements, than to incorporate a varied amount of "missing height" that changes as the tilt range of your head changes. Rather than trying to develop a set of equations to describe the amount of this missing height in your diagram, adding a small constant to the distance measured will resolve the issue.

Trying to keep track of the two elements of swivel isn't worth it when also dealing with laser clickover points and target visibility issues. It is easier to try to keep track of where the eyeball is in two horizontal planes, one established to measure the crown and the other for the base. However, I hesitate to try to explain all this to members on the list. They are probably pretty confused as it is, even for those who should be able to follow the subtle points. It has taken my friend Don Bertolette literally years to get off the forestry tangent method.

Bob Leverett writes:

Ed,

You're having to work at this too hard, my friend. Both Will and I understand what you are saying and concur that if one can do the measuring from a fixed swivel point in the head (with no concomitant eye rotation), the triangles and calculations are exactly as you depict. The vertical distance between successive positions of the eye is accounted for by the common vertex as you've explained. I've never not understood that point. The mechanical swivel of the head may not work perfectly for a number of anatomical reasons, but I'm willing to assume that it works well enough to allow the common vertex model to be applied in a percentage of measuring situations. But for those of us who have mesasured literally thousands of trees, we had to long ago abandon the common vertex model, because in-forest measuring conditions often require shifting one's position. This need gave rise to the two independent triangle solution and parallel planes concept that we'v e been following.

The earliest reason for abandoning the two dependent triangle solution administered from a fixed head (swivel point) position was the need to move forward or backward to get click-over points for the crown and base. Click-over does not necessarily occur at the same location for both crown and base. A second reason for abandoning the fixed head solution was that some shifting head movement, both laterally and vertically, became necessary to get the laser to return bounces. This is now even more true with the TruPulse line. Intervening clutter between laser and target has always presented a challenge to the measurer, and it seems the more expensive the laser, the more the laser is influenced by clutter. Should be the other way around. Some models allow you to ignore bounces out to a particular distance, but in the immediate area of the target, this feature is no solution.

The bottom line to the above discussion is that Will and I were forced to focus on the two independent triangle solution as a practical necessity for in-forest measuring. However, we haven't always carried through with this theme when drawing our tree-measuring diagrams. I've talked the solution through in many e-mails, but have not specifically included emphasizing the independent triangle solution that results in a shifting location for point A in my diagrams. In my diagrams, it looks as if we are maintaining the eye (really the head swivel point) in a fixed location. But for the reason just given, that is frequently not the case and needs be so explained in the ENTS methodology. Lots of new diagrams to draw, I guess.

To be thorough in dendromorphometry, we should address all situations, including the one where point A remains fixed in space, thus allowing the fixed distance add-on to compensate for dropping of the eyeball, i.e. the situation depicted in your diagram. However, there is one added complication to this method. The eyeball moves in its socket independent of head swivel and that effects the triangles. For the sake of argument, let's assume the distance from the eyeball to the point of head swivel is six inches. As you've duly noted, that distance doesn't change regardless of how we orient our head. Let's also assume that when standing with head erect, the line connecting eyball to point A of head swivel is level. It may not be exactly level. but it is close enough for these discussions. If the crown target is at an angle of 30 degrees, above eye level and the base target is 15 degrees below eye level, then there are 3 ways to sight to the crown and base targets. We can keep our sighting eye fixed in its socket and swivel our head 30 degrees up, take a reading, and then swivel our head down to 15 degrees below eye level and take the base reading. Since inn this scenario all movement to get the target and eye in alignment is through head swivel, the diagram that you drew works and the extension of the legs of the upper and lower triangles to point A takes care of the intervening vertical distance of eye position drop. However, we can also swivel our eyes in there sockets without swiveling our head - even if slightly uncomfortable. In this case the line from eyeball to point A remains level whereas the line from target to eye is at 30 degrees for the crown point and 15 degrees for the base point. There is no longer a straight line from target to eye and back to point A. The third scenario is some swivel of both, i.e some eye swivel and some head swivel. In early measuring situat ions, I tried to implement the first option as much as possible - only eye swivel. In that case, I swiveled the clinometer up and down and rotated my eye accordingly. That works for narrow angular spreads, but not wide ones. It is much easier to see with some head swivel. I suppose my alignment runs about 75% head swivel and 25% eyeball rotation.

Bob

Bob Leverett writes:

Ed,

I now understand your point that the triangles can be independent and that you are just compensating for the vertical effect of head swivel either above or below the point of swivel - treated independently. At first it appeared to me that concurrent eye swivel would be a complicating factor. If there is no concurrent eye swivel, I accept your construct. Of course, if there is no head swivel, then there is no additive. If there is both head and eye swivel, I need to draw a diagram out and convince myself that there is no counteracting effect. I'll make the drawing and pass it to you and Will tomorrow.

Bob

From: "Edward Frank" <edfrank@comcast.net>

Bob,

You have been talking about the actual field conditions where you are at times forced to move your head back and forth, up or down, or sideways in order to get a better shot or to find a click over point. These are all sources of potential error. But these are not error related to head swivel, but a different category of error. My theoretical idea may not be applicable in the field, but it does fix all of the lost height errors on paper. Sorry for harping on this point, I wish I had never brought it up.

Ed,

Actually, I'm glad you did. It is forcing me to rethink the whole measuring process and isolate sources of error and consider solutions. I'm satisfied with your logic. I hadn't given it sufficient thought before because of the multitude of other problems we have to contend with in clutter measurement situations, but you are correct and I'll be noting that in an upcoming e-mail to the list.

Teasing apart the sources of error and their individual and collective effects is an indispensible part of what we do. We have to keep each other honest. That's what makes us a great team.

Bob

Ed and Will,

I've attached a diagram to illustrate the impact of having both head and eye swivel. I put this together pretty quickly. I don't think I made any errors in logic. Maybe the two of you can troubleshoot the diagram and its associated logic. My contention is that eye swivel necessarily changes the calculations. If there is only head swivel, then the addition of the distance from eye to point of head swivel to the rangefinder distance compensates for the vertical movement of the head from the horizontal position in the calculation. But swiveling the eye to see the target steepens the angle and we no longer have a straight line from the point of head swivel, through the eyeball, to the target. The diagram indicates that adding more swivel from the eye on top of head swivel negates the simple addon of the eye to head swivel point distance to what the rangefinder reads. The measurement environment becomes more complicated. I can further strengthen this diagram if it would help, such as exaggerate the angles to make the distance components stand out better.

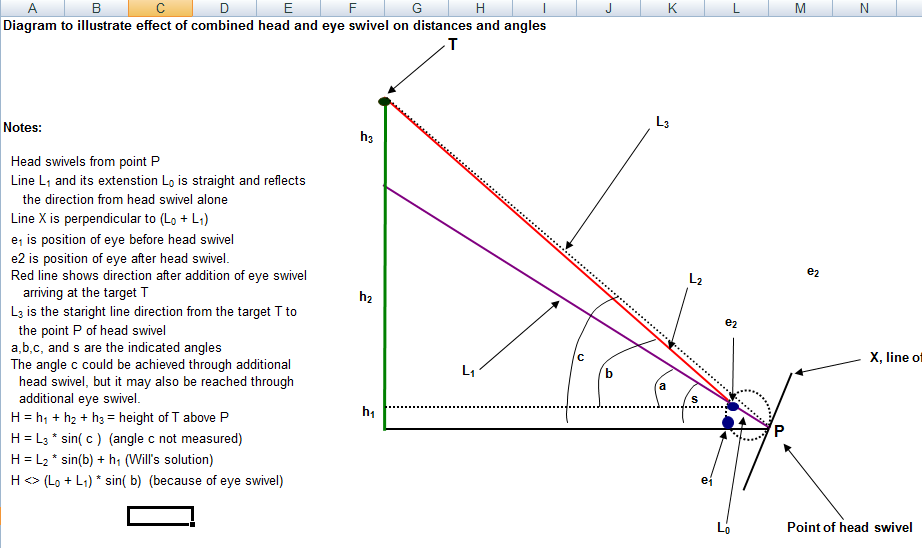
From: "Edward Frank" <edfrank@comcast.net>

Bob,

Thanks for the diagram. I think you already exaggerated the effects of eye swivel beyond the point of reasonableness, so there is no need to further exaggerate it to make things "clearer." I don't really believe that you are swiveling your eye that much when actually making the measurement because it is uncomfortable to painful to do so. In any case the projection of the eye-swivel line to the horizontal plane versus the head-pivot line to the horizontal plane is a small difference in additional length when compared to the baseline length to the top of the tree, a small difference when compared to each other, and a small difference when compared to the height you have marked h1. This difference becomes smaller with less eye-swivel and as the angle to the top decreases in steepness.

The question that really needs to be addressed is not minutia about the pivot point and the eye swivel, but when you are looking at the independent triangles for the top and bottom - how are they related to each other? Do you look at them from the same position? If you are you need to account for h1 in both the top and bottom triangles. When you move, how do you determine whether or not you have moved upward or downward between the shots? Are you looking to determine whether vertical movement has occurred based upon what you see when looking horizontally at the tree? If you are then the h1 component in both the top and bottom triangles should be included in the height calculation, rather than simply ignoring it. Overall it would result in a more accurate measurement in the few cases where that small height would make a meaningful difference. If you are adjusting the relative positions of the two triangles to make up for the offset betw een them, then you should not. If you are ignoring it, that is also a reasonable and practical solution for actual field use. If you are writing it up for publication and looking at all of the potential sources of error in the measurements then you need to analyze it and address it in some way.

Bob Leverett writes (May 19, 2008)

Ed,

I expect that a maximum impact of eye swivel occurs at about an added angle of 10 degrees, 15 at the most for the reason you state- i.e. discomfort. I am admittedly reaching a bit on this diagram. We may conclude that the impact of eye swivel can be ignored, but that needs to be confirmed. I think Will is considering that question further and will await what he finds.

My point has been, and continues to be, that from a practical standpoint you must often shift (and consequently track) your head movement when measuring trees in a closed canopy forest. Keeping tracking of where the level line lies in space through the head swivel point as opposed to eyeball for the purpose of compensating for the raising or lowering of the eye from the head swivel position makes sense most when that location of the head swivel point doesn't shift out of its initial horizontal plane. Then adding the extra eye to point of swivel distance as a constant on to the laser distances for both the above eye and below eye situations accomplishes the desired result without having to keep track of an upward or downward shifting eye position - as your have correctly pointed out.

In terms of effects, Ed, the devil is in the details. If you have to shift your eye up or down more than occurs from mere head swivel, you must to track that vertical displacement and distinguish it from the component attributable to just head movement (if you are compensating for the latter by the add on distance), which means you have to keep track of the total vertical displacement and then subtract out the part attributable to head swivel that you already to into consideration from the addon factor to laser distance. From this state of affairs, you are better of tracking the total vertical eye movement as oppsoed to teasing out the individual components and treating them separately. This is what Will was originally getting at in his diagram.

As I admittedly previously, my previous diagrams make it appear as if the eye stays fixed in the initial horizontal plane through the eye position and ignores its change of position due to head swivel. This is a regrettable oversimplification of what occurs in the field. With multiple reasons for head movement in the difficult measuring situations, it becomes easiest to track total up and/or down eye postion rather than attempt to treat the sources of movement separately. That will remain the case.

However, when I measure a tree in the open with good concurrent visibility of the crown and base, where there is no reason to shift my head up or down, changing eye postion only from head swivel, your solution to compensating for the up and/or down movement of my eye due to head swivel will be incorporated in my standard measuremnt protocal.

Methods for tracking total head moevement will be addressed in the dendromorphometry book. But better that the discussion be taking place now than being identified as missing in the book.

Bob

Home