Problem #9: This problem was suggested by Ed Frank. It is a counterpart to problem #8, which deals with two problems: (1) calculating the volume achieved at a particular height above the base of a cone, and (2) calculating the height at which a specified percentage of the total cone’s volume is achieved.
Ed presented an image of one of Larry Tuccei’s huge live oaks. The image suggested a big dome of hemisphere. The question arises as to how much space such a shape consumes. The formula for a hemisphere is
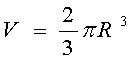
Four problem types emerge from considering the hemisphere that will be of interest to ENTS. The first problem is the simple calculation of the volume of the hemisphere. The answer involves the application of the preceding formula. Type two problem focuses on how far we must go from the base to be at a designated point on the surface of the hemisphere. This problem is also easily solved. If a =angle to point from trunk of tree and R is the radius of the hemisphere, then the horizontal distance h is given by
![]()
The third problem type involves determining the volume achieved at a specified height above the base of the hemisphere. The following formula computes Vp, the volume at the specified height h. The formula is derived with the help of integral calculus, but its use is straightforward.
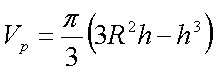 |
The last problem involves specifying a percent p of volume and determining the height h at which that percent is achieved. The mathematical process required is not simple. For explanation purposes, it is outlined below. However, an accompanying Excel workbook is provided to automate the process. We start the process with the following equation.
This equation is called a reduced cubic where R, p, and h are defined as above. The solution requires that we compute the following quantities in the order shown.
![]()
![]()
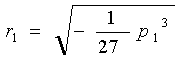
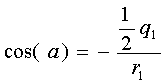
From p1, q1, r1, and cos(a), we can compute the roots of the cubic equation through the following equations. We designate the roots as h1, h2, and h3.
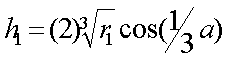 |
|||
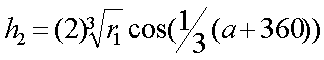 |
|||
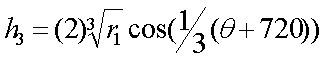 |
|||
In general, only one of the roots will be
applicable to the problem, i.e. only one root will lie in the range ![]() . The other roots
are algebraically valid.
. The other roots
are algebraically valid.
As mentioned, an Excel workbook is being provided to automate the process. The spreadsheet entitled ProblemSolver allows the user to enter R and/or h and p to calculate the desired quantities. The green cells are for user input. All other cells are protected.
Summary Comments: This problem is being presented as a companion to problem #8. While an explanation is given for the problem that may stretch members a bit too far without a background in mathematics, it should be kept in mind that an understanding of the problem and use of the Excel solution is all that is required.
measure/problems/Problem_9.xls