Problem #16: The crown of a tree is to be treated as a frustum of the ellipsoid shape. The lower base of the frustum is taken from either the midpoint of the ellipsoid or above the midpoint. The upper base is to be the top of the ellipsoid. This means that the upper base is a single point instead of a plane surface. If we designate the semi-major and semi-minor axes of the lower base of the frustum as A and B and the height of the frustum as H, we can use a formula to compute the volume of the frustum of the ellipsoid.

Solution: The accompanying diagram shows the solution to the problem. The top of the frustum in the diagram below is the top of the ellipsoid. The blue ellipse is the middle of the frustum and the red ellipse is the lower base of the frustum.

Summary comments: The above solution works for any geometrical solid of revolution of degree three or less, which includes solids such as spheres, parabolas, hyperbolas, ellipsoids, cylinders, and cones. Note that the lower base of the frustum starts starts at the midpoint of the solid and goes to the top. In the above diagram, semi-major and semi-minor axes a and b are at the midpoint of the frustum. The challenge is to obtain the measurements to pass to this model.

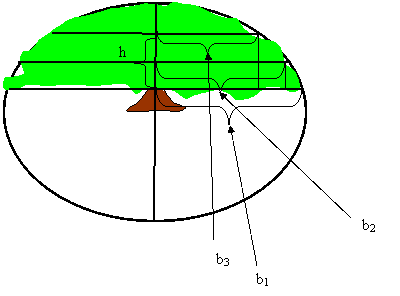
            A variation on the above configuration is illustrated in the diagram below where the top of the frustum is not taken as the apex of the solid.  The slice shows the semi-minor axes designated as b₁, b₂, and b₃. A comparable slice at right angles would yield the semi-major axes a₁, a₂, and a_3.

The volume formula for the frustum is as follows

Summary comments: Note that in the above diagram b₂ reflects the semi-major axis at the midpoint of the frustum as previously explained. In general, the formula

applies to any geometric solid, the surface of which is generated by a polynomial of not greater than 3.