Problem #15: Larry Tucei Jr. discovers another fine southern live oak and wants to measure the volume of the space taken up by the crown projected to ground level and to measure the perimeter of the crown also projected to ground level. For whatever reason, Larry is unable to walk the full perimeter of the crown. Larry determines the height of the tree as 62 feet, the crown spread in one direction as 125 feet and 95 feet in the direction at right angles to the first. Looking at the shape of the live oak from a distance, its profile looks elliptical to Larry and suggests to him the ellipsoid form as best fitting the tree’s overall shape. From the three measurements, he took, how can Larry measure the volume of the space occupied by the tree and the perimeter of its crown projected to ground level?

Solution: The diagram and formulas below show how to make the calculations. The accompanying Excel workbook shows the calculations and provides an automated solution for values of a, b, and c.

Definitions

P=perimeter of ellipse in the ab plane

V=volume of ellipsoid

V_s=volume of half of ellipsoid

a=semi-major axis of ellipse in ab plane

b=semi-minor axis of ellipse in ab plane

c=semi-minor axis of ellipse in ac plane

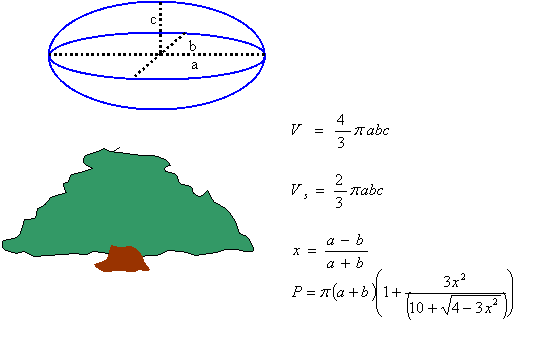
Summary Comments: Trees such as the southern live oak strongly suggest that we abandon the simple height, average crown spread, and trunk circumference measurements as the standard. Crown volume, crown perimeter, longest limb, trunk volume, etc. are needed to do justice to these great trees. While calculating the above with accuracy takes a large amount of work, approximations can be made for many trees. This problem illustrates the use of the ellipsoid shape to make the calculations of volume and perimeter. The accompanying Excel workbook automates the calculations and follows the same format as prior workbooks. The ProblemSolver spreadsheet automates the process.

measure/problems/Problem_15.xls