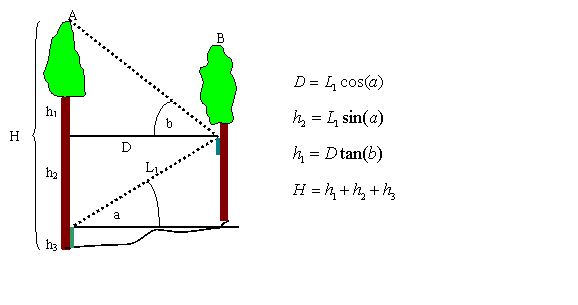
Problem #14: Two trees are located in proximity to one another. We will call them A and B. Both have straight, vertical trunks. The objective is to measure the height of tree A. We assume that A’s top is directly over its base. We further assume that the top of A cannot be seen from any ground-based vantage point. A climber climbs up into B to a point where the top of A is visible. The measurer gets positioned at the base of A. The climber is visible to the measurer. The climber has only a clinometer and the measurer has both a clinometer and laser rangefinder. The climber calls down the angle to the top of A from the vantage point in B. If the assumption that the top of A is directly over its base is fulfilled, how can the measurer measure the full height of A from the location at the base of A?

Solution: The definitions and diagram below shows the solution to the problem.

Definitions

h₁=height of A above climbers eye

h₂=height of climbers eye above

        measurer's eye

h₃=measurer's height

L₁=distance from measurer's eye to

        climbers's eye

D=horizontal distance between trunks

      of A and B

H=height of A

Summary Comments: It does not matter where the base of B is to the solution of this problem.