Problem #12: A tree growing near the bottom of a ravine is to be measured for its height. The measurer has a clinometer and tape, but no laser. From the side of the ravine, the measurer looks down toward the base, which cannot be reached, and upward toward the crown. The measurer is able to line up the high point of the crown with the trunk from a spot on the side of the ravine having uniform, linear slope. How might the measurer determine the height of the tree, using an exterior baseline and angles to the top of the tree from the ends of the baseline and the angle to the bottom from the lower end of the baseline.
Solution: Diagrams and accompanying equations will illustrate the solution. Angles a1, a2, a3, and a7 †as defined above are measured by the measurer - also distance d. Angles a4, a5, and a6 are computed using the rule that the angles of a plane triangle add up to 180 degrees. The length of side L of the triangle from the measurerís eye to the crown-point, then down to eye level, and back to the eye is computed using the law of sines that says that the ratios of a sides of the triangle to the sines of the respective angles are all equal. Therefore, if A, B, and C are the sides of a triangle and the opposite angles are designated by a, b, and c, then the law of sines is illustrated below. The law of sines illustration is followed by the tree diagram.
†††††††††††††††††††††††††††††††††††††††††† 
††††††††††††††††††††††††††††††††††††††† 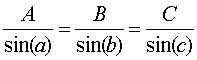
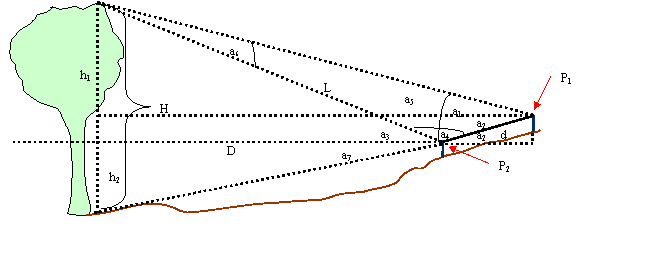
Tree Diagram
†††††††††††
††††††††††† In the above diagram, H = full tree height, h1 = height above eye level and h2=height below eye level.
Derivation of equations and calculation of tree height
††††††††††† In the above diagram, let L be the distance from the eye to the high point of the crown. †† Then by the law of sines
††††††††††† In the above diagram, let D be the level distance from the eye to a point directly beneath the highpoint of the crown.
†††††††††† ![]()
††††††††††† By algebraic substitution, we can derive a formula for H that involves only the known quantities angles a1, a2, a3, and a7 and distance d.
 |
Summary comments: If a2=0, the baseline is level, so the formula for H serves two measurement scenarios, i.e. where P1 is above P2 and where they are on the same level. An Excel workbook accompanies this problem that automates the solution.
measure/problems/Problem_12.xls