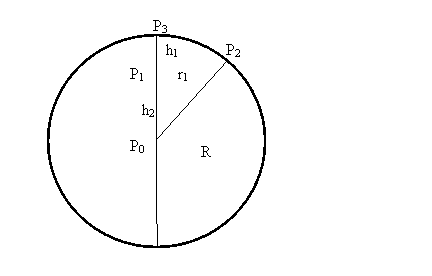
Problem #11: This problem is related to problem #9. The objective is to calculate the volume of part of a hemisphere starting at the apex and going down for a distance of h₁. This problem was suggested by Ed Frank. At the start, the radius of the hemisphere is not known. The diagram below shows the part of the hemisphere of interest.

Ed Frank’s description that motivates the above drawing follows.

“Think of the hemisphere partially buried in the ground.  The shape of the tree canopy is the part that is sticking out.  There is a height h₁ which is the height of the part sticking out of the ground.  In a tree this is the height of the tree.  h₁ = R- h₂   There is also r₁ which is the pseudo- radius of the hemisphere at the point it intersects the ground surface as measured from the center of the circle at ground level to the edge of the circle.  This is the crown spread divided by two.” 

            The portion above the brown line is the area of interest, i.e the part of the hemisphere above ground. The volume of the area above the brown line is what we want to determine.

Solution: The definitions and equations below show how to solve the problem.

Definitions
	R = radius of hemisphere (unknown)
	h1 = distance from top of hemisphere to point P1, i.e. P1 to P3
	r1 = distance P1 to P2
	h2 = distance from P0 to P1
	Vq = volume of hemisphere from P3 to P1
	Vp = volume of hemisphere frpm P0 to P1
	V = volume of hemisphere

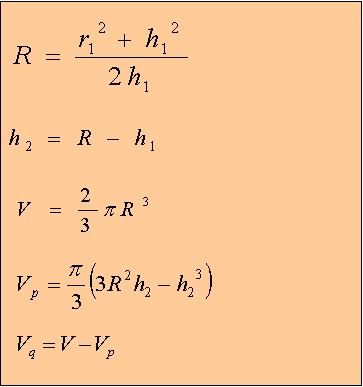
measure/problems/Problem_11.xls