|
==============================================================================
TOPIC: A mini-study
http://groups.google.com/group/entstrees/browse_thread/thread/3b95301bd02ad60e?hl=en
==============================================================================
== 1 of 3 ==
Date: Fri, Jun 6 2008 2:15 pm
From: dbhguru@comcast.net
ENTS,
I apologize if this email was sent yesterday. I didn't see it show
up in my inbox or sentbox, so I'm forwarding it again from my
draftbox with proper editing and additions of course.
Yesterday, after an earlier walk in the woods behind Monica's house,
I went to Child's Memorial Park to do a mini-study of the tangent
method of measuring the height of a tree height from different
locations. I wanted to illustrate a point, which will become clear
by the end of this email. For the mini-study, I chose a sample of 6
trees: white pine, a pin oak, a sugar maple, a white fir, a white
oak, and a red maple. Trees were initially selected for the
unobstructed view of their crowns over transects of 67 to 150 feet.
However, the white oak and red maple proved to have obstructions at
particular distances along their transects, so the transects for
them were truncated.
For each sample tree I first determined the highest point using the
TruPulse 360. I spent from 5 to 10 minutes on each tree with my
TruPulse set in VD mode. I did plenty of cross-checking of the
highest point of each tree from many directions. The absolute
heights were determined to +/- 0.25 feet. The following table shows
study results. BTW, I got the idea for using the transect method and
comparing tangent-based heights at pre-established points along the
transect from Dr. Don Bragg. Don is applying the method in a more
complete fashion than what I did yesterdaay. He uses 4 transects per
tree, approaching the tree from the cardinal compass directions.
This enables him to evaluate the reliability of averaging heights
taken from different directions via the tangent method to compensate
for the problems with that technique. ENTS is covering all bases.
| Species |
Distance |
Tan Hgt |
True Hgt |
Diff |
Avg |
| WP |
150.0 |
104.5 |
101.5 |
3.0 |
|
| WP |
125.0 |
104.1 |
101.5 |
2.6 |
|
| WP |
100.0 |
106.8 |
101.5 |
5.3 |
|
| WP |
75.0 |
112.9 |
101.5 |
11.4 |
|
| WP |
67.0 |
114.8 |
101.5 |
13.3 |
7.1 |
| PO |
150.0 |
97.7 |
91.5 |
6.2 |
|
| PO |
125.0 |
99.6 |
91.5 |
8.1 |
|
| PO |
100.0 |
100.8 |
91.5 |
9.3 |
|
| PO |
75.0 |
107.5 |
91.5 |
16.0 |
|
| PO |
67.0 |
113.4 |
91.5 |
21.9 |
12.3 |
| SM |
150.0 |
87.3 |
81.5 |
5.8 |
|
| SM |
125.0 |
87.5 |
81.5 |
6.0 |
|
| SM |
100.0 |
90.0 |
81.5 |
8.5 |
|
| SM |
75.0 |
93.3 |
81.5 |
11.8 |
|
| SM |
67.0 |
95.2 |
81.5 |
13.7 |
9.2 |
| WF |
150.0 |
87.0 |
78.5 |
8.5 |
|
| WF |
125.0 |
88.6 |
78.5 |
10.1 |
|
| WF |
100.0 |
91.2 |
78.5 |
12.7 |
|
| WF |
75.0 |
97.2 |
78.5 |
18.7 |
|
| WF |
67.0 |
99.4 |
78.5 |
20.9 |
14.2 |
| WO |
150.0 |
90.3 |
82.5 |
7.8 |
|
| WO |
125.0 |
91.1 |
82.5 |
8.6 |
|
| WO |
100.0 |
93.0 |
82.5 |
10.5 |
|
| WO |
75.0 |
103.6 |
82.5 |
21.1 |
13.8 |
| RM |
100.0 |
87.6 |
74.0 |
13.6 |
|
| RM |
75.0 |
93.5 |
74.0 |
19.5 |
|
| RM |
67.0 |
95.1 |
74.0 |
21.1 |
18.1 |
|
|
|
|
|
|
|
|
|
|
|
|
| Overall
average |
|
|
|
11.7 |
Although this mini-study involves a small sample of trees. study
results tell the basic story. By the compensation methods/techniques
we have discussed on this list (cross-triangulation, lateral offset
ala Don Bertolette) for the tangent method, measurement errors can
be reduced. There is no argument about that. Never has been. But
applying the tangent method without reducing the error risk leaves
the technique unsound for scientific use - unless accuracy isn't a
concern.
With the tangent method, ideally, one first seeks to locate the
vertical projection of the crown point to eye level and then adjusts
the baseline accordingly. If this method is done successfully, the
tangent method is as relibale as the sine method. But it is often
practically difficult to implement for reasons I'll be happy to
discuss, should anyone want to continue in that direction.
As an alternative to crown point cross-triangulation, Don
Bertolette's method can substantially reduce the risk or error, but
extra time must be taken, and in some cases, the error can still be
too much. Getting oneself positioned so that the crown point is in a
laterally location requires experience.
Taking the discussion one step farther, I have no problem
acknowledging that a subset of species and of tree forms do lend
themselves acceptably to the shortcut tangent method applied without
mitigation, but the risk of substantial error is always present. The
full story of what the mini-study exhibits to a degree will be told
in full in the paper being coauthored by Lee Frelich, Don Bragg,
Will Blozan, and myself. Lee will be the principal author. Now to a
different subject.
Early yesterday morning, Gary Beluzo and I walked up Broad Brook
searching for tuliptrees. Along the way, I remeasured the tall,
double white pine found originally by Will Blozan last October. I
had to use my Nikon Prostaff 440 for distance because the canopy is
too closed to allow me to use the TruPulse effectively. I can't
shoot through the smaller gaps that are now available to me with the
thick late spring foliage. Well, the height of my pine, with some
new growth, is 136.3 feet. Looking at the new growth candle, and
considering my pre-growth measurment, I'd say the height of the big
tree is 136.0 feet. Regardless, I get a deep sense of satisfaction
of being able to stand at the foot of a tree in the above 130-foot
class so near to my home. The next closest population of 130-footers
is Look Park, about a mile away. Then comes several trees on the
Smith College campus, about 3 miles distant. Going to the south,
there is a sma ll cluster in Easthampton, a bit farther, with on
e pine at the site very close to 140. Still farther, about 7 miles
distant, there is a more substantial population of 130-footers in
the Mount Tom State Reservation. One tree will likely reach 140 this
growing season. Going westward, there are a couple of 130-footers on
an Audubon Sanctuary a few miles distant and there is a cluster of
130-foot tall pines in Williamsburg on Petticoat Hill about 7 miles
away. But the closest group of really tall white pines is on the
Bryant Homestead, about 22 miles distant. It is there that pines
break the magic 150 threshold. Six pines have been confirmed at over
150 feet. With luck one tree will top 158 at the end of this growing
season. I swell up with pride everytime I think of those pines.
Still farther distant, but under one hour's drive, there is the
unsurpassed MTSF, with at least 85 pines over 150 feet. Mohawk has
only one competitor in all New England and that is a private site in
Claremont New Hampshire.
In some ways, my renewed appreciation of tall white pines is a
continuing reaction to the cutover woodlands of interior Maine, and
the more aesthetic, but still short trees of the coastal region. I
haven't given up on Maine. Monica and I plan to return, but it nice
to walk in that present visitors with canopies with 100-foot tall
and taller trees. The high canopy is inspiring in ways that are hard
to express. You feel it.
Little Broad Brook, running behind my wife's house, has turned out
to harbor a most satisfying patch of woods, an almost inspiring
forest, a forest that few souls explore these days or appreciate. As
a consequence, Monica and I have our own private woodland sanctuary.
The Broad Brook woods may not be the southern Appalachians, nor even
the slightest potential to become like those distant forests, but
the woodlands bordering that quaint little stream is more than
earning its pay these days. Its 114.7 Rucker Index will likely go to
115.0 by the end of summer. In the bigger scheme of eastern forests
from Canada to Florida, that's not bad, especially when it is in
your back yard.
Bob
== 3 of 3 ==
Date: Fri, Jun 6 2008 10:51 pm
From: "Edward Frank"
Bob,
Things are never as simple as they appear, but although not likely
practical in the field, thinking about this there is a simple
geometric solution to determining tree height by making two
measurements 180 degrees apart. On level ground, from one side find
the top of the tree, measure the angle to the top and the distance
to the center of the base of the trunk. From a position 180 degrees
away on the other side of the tree find the same top. Move inward
and outward until the angle to the top for this side is the same as
measured on the first side. measure the distance to the center of
the trunk. Calculate the height as measured from both sides. Average
the two together to obtain the true height of the top. If the top is
offset in any part toward or away from the center the amount it
appears higher on one side will be exactly offset by the amount it
appears lower on the other. the errors would exactly offset.
Ed
== 2 of 11 ==
Date: Sat, Jun 7 2008 4:46 am
From: dbhguru@comcast.net
James,
Indeed I do. Chasing large, tall white pines has been a specialty of
both Will and myself for years. I am especially beholding to Pinus
strobus. Without the contribution of that noble species, the forests
much above 42 degrees north latitude in New England would be
shortchanged when the notion of stateliness is invoked. While I
strongly believe that the size of the past great pines of Vermont,
New Hampshire, and Maine have been exaggerated in anecdotal accounts
for both heights and girths, I believe there were plenty of stands
with 150-footers. The possibility of taller trees in Massachusetts
and Connecticut is still an unknown. For the larger pines, girths of
12-13 feet would not have been uncommon in all New England states.
But above those dimensions, the pickings would have been slim. Past
accounts of giants are misleading mainly because when people see
pines 12-13 feet around, they often estimate the pines to be at
least 6 feet in diameter. Over-estimation of diameter by
1 to 2 feet is common.
Thinking in terms of the full range of the great whites, based on
what we've seen to this point in time, the tallest white pines were
and still are in the southern Appalachians. Pennsylvania and
possibly Wisconsin may have matched the southern skyscrapers, but it
isn't clear that that is the case. We just don't know. It is fun to
speculate though.
We're still searching for the illusive 200-footer. Outside the
Boogerman Pine, we've never breeched that threshold in the East. It
is exciting to think that somewhere out there in the vastness of the
southern Apps, another one lurks. Similarly, in New England, I still
hold out hope to break 170, but the odds are very slim. What passes
for forest management up here on private lands doesn't entertain the
idea of leaving a few trees with the potential to achieve great
height or girth. On public lands, if a tall tree site isn't
currently protected, then the odds of pines beling allowed to reach
their maximum potential don't look good.
Bob
-------------- Original message --------------
From: James Parton
>
> Bob,
>
> Don't ya love those white pines!?
>
> JP
>
== 4 of 11 ==
Date: Sat, Jun 7 2008 5:46 am
From: dbhguru@comcast.net
Ed,
You are 100% correct. The attached spreadsheet gives a quick
algebraic proof of your hypothesis. It is well worth including in
the dendromorphometry book as a trick of the trade. As you point
out, it may be difficult to apply in the field, but it is sound
theoretically. The assumption in the attached diagram is that the
crown point, trunk, and measurer are all in alignment.
Bob

== 5 of 11 ==
Date: Sat, Jun 7 2008 9:00 am
From: "Edward Frank"
Bob,
Cool. On your diagram you should extend the trunk upward and project
the two sighting lines to the trunk. This will form two similar
triangles the same size one showing the projection of how the right
side overestimates the height, and the the other showing the left
side projection underestimating the height. If the true top, the
trunk and the measurers are not in line the difference would only be
the difference in length between the slightly rotated angle to the
top and the angle to the upward projection of the base of the tree.
With a reasonable base length and an offset of ten feet or so (or
less) the difference in rotating the measurement lines from the
trunk base projection would make a difference, but only on the order
of a few inches.
Ed
== 6 of 11 ==
Date: Sat, Jun 7 2008 9:20 am
From: "Edward Frank"
Bob
That did not come out right- If the true top, the trunk and the
measurers are not in line the difference would only be the
difference in length between the slightly rotated angle to the
[projection of ] top and ...... the [distance to] base of the tree.
With a reasonable base length and an offset of ten feet or so (or
less) the difference in rotating the measurement lines from the
trunk base projection would make a difference, but only on the order
of a few inches. The base line in the calculation is the average of
the distances to the trunk from each side of the tree, and the angle
would be the vertical angle measured from each side.
Ed
== 8 of 11 ==
Date: Sat, Jun 7 2008 11:51 am
From: "Will Blozan"
Bob,
One suggestion: I think you should use the forestry convention of
chains as
well for this examination. Some clinometers are based on chains from
the
tree so using 66' and 132' would be a very valuable addition. This
would
allow better interpretation by those accustomed to those units.
Will
== 9 of 11 ==
Date: Sat, Jun 7 2008 12:43 pm
From: dbhguru@comcast.net
Will,
Good suggestion. In a future version of this experiment, I'll add 66
and 132 -foot baselines.
For all to think about from reviewing the data, short baselines are
extraordinarily risky. All members of the ENTS high priest-priestesshood
know that. Also, several measurements taken from different
directions, all on short baselines, does not guarantee an
improvement over a single measurement. In the case of using the sine
method, you don't necessarily improve the accuracy relative to the
absolute top of the tree - since you may not be seeeing it. What you
are guaranteed of is that the points you do measure are not subject
to the crown offset error. This is an extremely critical point to
understand when thinking about all phases and facets of the
measuring process.
Bob
== 10 of 11 ==
Date: Sat, Jun 7 2008 1:00 pm
From: DON BERTOLETTE
Bob/Will-
Great, I can dust off my topographic abney
-DonRB
==============================================================================
TOPIC: A mini-study
http://groups.google.com/group/entstrees/browse_thread/thread/3b95301bd02ad60e?hl=en
==============================================================================
== 1 of 4 ==
Date: Sun, Jun 8 2008 2:21 am
From: Beth Koebel
Bob,
I am curious but like the math know how, what
difference (error) would be made if the person did not
go 180 degrees from where the measured from but lets
say 170 degrees.
Beth
== 4 of 4 ==
Date: Sun, Jun 8 2008 6:09 pm
From: James Parton
Bob,
Yes, the forests would be really losing something if the White Pine
was to go. Here in the southern Apps, the White Pines are among the
most stately of trees. Among the conifers their only rivals are the
Eastern Hemlock, which is vanishing from many areas. Like you, I
enjoy
looking for tall ones. I have found 1 tree over 150 feet and 1 over
170. Of course I have visited the really tall pine forest in
Cataloochee Valley known by ENTS as Pine Flats ( during the "
moot " )
and I have visited the " Boog " several times. I would
have loved to
have seen it before it lost it's top. Yes, I feel that there are yet
some super pines out there that have not been found. Ones over the
Boogerman's current and possibly past height. They are rare but I
feel
it is still a real possibility. Will showed me on his computer
during
the entmoot where he thought some record Great Whites can be found,
on
the Tennessee side of the Great Smokies. If he ever gets the
opportunity to search out these trees and I can get the time off, or
we can do it on some extended holiday weekend, I would love to
accompany him on this great pine hunt. He might have to wait up on
me
a little though ~laughing~. We have mentioned doing a outing on
Congaree National Park. A pine hunt on this GSMNP area in Tenn that
Will knows of by ENTS would be great too. But one would have to be
physically fit enough to do it. That area looked pretty remote and
rugged. It may well kick my ass, but a possible " boog beater
" would
make it worthwhile. I am sure they are areas other than this with
huge
whites. All Ents keep their eyes open and their lasers handy....
James Parton
==============================================================================
TOPIC: Answer for Beth
http://groups.google.com/group/entstrees/browse_thread/thread/9526f2ef371c34db?hl=en
==============================================================================
== 1 of 1 ==
Date: Sun, Jun 8 2008 9:47 am
From: dbhguru@comcast.net
Beth,
I couldn't leave it alone. Diag2 of the attachment (second
spreadsheet) shows the algebraic derivation (with shortcuts taken
near the end) of what results in being a two step process to measure
height using tangent-based calculations from two points not in the
same line with the trunk. The diagram looks down from the top on the
field of measurement and shows that the observer's first position,
crown point, and trunk are in alignment. The observer's second
position is not on alignment with the crown point and trunk. More
specifically, assumptions made by this model include:
1. Angle to the crown point from each observer position is the same
(Ed's initial condition).
2. Eye level at each observer position is in the same horizontal
plane.
3. Observer position #1, crown point, and base of trunk are in same
vertical plane.
There are a number of methods that can be derived to triangulate the
crown point offset value. Collectively they reveal the work that is
required to make the tangent method work well enough in the field.
What is abundantly clear is that the shortcut method used with
clinometer and baseline if far too error-prone to ever be acceptable
to ENTS in our database. This having been said, it is fun to work
out mathematical solutions to specialized situations. Its all part
of what we do.
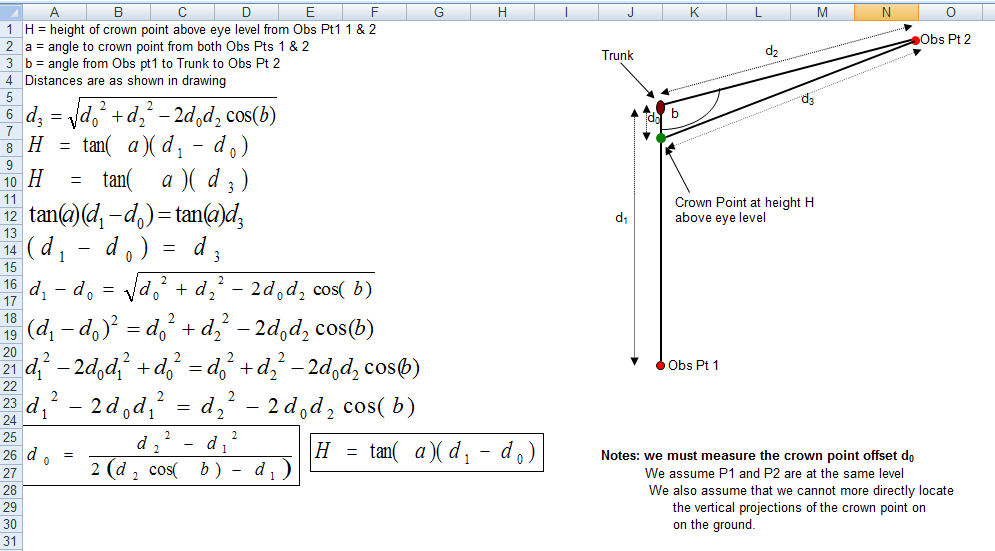
If the tangent method has to be used, the safest practical way in
the field is probably crown point cross-triangulation. Other methods
can work, but the assumptions behind the models must be fulfilled.
The biggest drawback to amateur use of the tangent method is a lack
of understanding of what assumptions go with each model and where
particular assumptions can be relaxed without doing unacceptable
damage.
Bob
==============================================================================
TOPIC: Another formula for Beth
http://groups.google.com/group/entstrees/browse_thread/thread/8e04a54c8fa7a758?hl=en
==============================================================================
== 1 of 1 ==
Date: Sun, Jun 8 2008 4:17 pm
From: dbhguru@comcast.net
Beth,
Many months back, I developed a fairly simple formula to be used by
folks with clinometers and tape measures only. Jess Riddle was kind
enough to note that the formula represented an advancement in our
search for new measuring techniques to fit every budget. The formula
measures the vertical height of a crown point above eye level.
Assuming level ground, the measurer takes the angle of the crown
point from a convenient location, backs up a distance of 20 feet or
more and takes a second angle of the same point and then applies the
formula below.
Let:
H = height of crown point above eye level
D = length of baseline between two observation points
A = angle from eye to crown from closer vantage point
B = angle from eye to crown from more distant vantage point
H = [D * tan(A)*tan(B) ] / [tan(A) - tan(B)]
This method does not require that the two measuring locations and
the crown point be in alignment with the trunk.
If we take:
(1) the above method,
(2) crown point cross-triangulation as explained in Will Blozan's
tree measuring guide,
(3) the clever averaging method proposed by Ed Frank several days
ago, and
(4) Don Bertolette's lateral offset approximation method
we have a set of measuring methods for folks to use while they are
saving their pennies for a laser rangefinder and clinometer
combination.
With respect to the method presented above, if the two observation
points are not on the same level, adjustments in the formula render
it too cumbersome to be used by most measurers. So I won't present
the modified formulas in this communication.
I trust that any new members who may be playing catchup with our
measuring techniques by reading emails on the website about
measuring are absorbing the all important lesson that the right
model needs to be chosen for each set of circumstances.
Bob
|